#PBZOJ4751. 邋遢大王
邋遢大王
题目描述
给出一个 n 行 m 列的点阵,每个点的半径忽略不计,问最少需要多少条有向直线段,使得它们首尾相连不间断组
成的有向折线能够将点阵中所有的点都至少穿过一次,且每条有向直线段至少经过点阵中的两个点。为了确保你给
出的答案是正确的,请给出任意一组解。假设点阵左上角点的坐标为 (1,1) ,点阵右下角点的坐标为 (n,m) ,点
阵第 i 行第 j 列点的坐标为 (i,j) ,你需要依次给出有向折线上每一条有向直线段经过的点集(详细的说明参
见输出格式)。下图给出了样例对应的一组解:
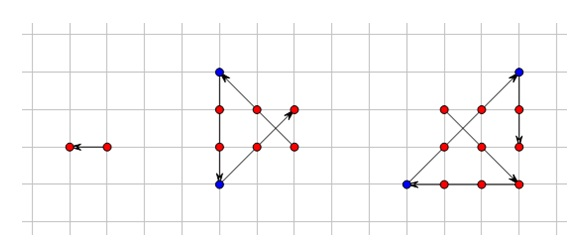
输入格式
第一行包含一个正整数 T ,表示有 T 组测试数据。
接下来依次给出每组测试数据。对于每组测试数据:
仅一行,包含两个正整数 n 和 m 。
保证在一行中的每个整数之间有恰好一个空格,没有其他额外的空格。
保证不超过 10 组数据满足 n>10 或 m>10 。
100% 的数据满足:1≤T≤100,1≤n,m≤1000,nm>1
输出格式
对于每组数据输出 L+1 行,第一行包含一个正整数 L ,表示折线的最少条数,随后的 L 行按照连线顺序依次给
出折线的每一部分,其中第 i 行输出四个正整数 ax_i,ay_i,bx_i,by_i ,满足 1≤ax_i,bx_i≤n,1≤ay_i,by_i
≤m ,表示折线的第 i 条有向直线段最先经过的点是 (ax_i,ay_i) ,最后一个经过的点是 (bx_i,by_i ) 。
对于本题,输出中在一行的每个整数之间用恰好一个空格隔开,不能有其他额外空格。
注意:折线的起点可以不是 (1,1) ,而且对于 i=1,2,?,L-1 ,若折线的第 i 个拐点在给出的点上
则需要满足 bx_i=ax_(i+1) 且 by_i=ay_(i+1) ,否则不需要满足。
3
1 2
2 3
3 3
1
1 2 1 1
3
2 3 1 2
1 1 2 1
2 2 1 3
4
1 1 3 3
3 3 3 1
2 1 1 2
1 3 2 3

