#PBZOJ2521. 最小生成树
最小生成树
题目描述
Secsa最近对最小生成树问题特别感兴趣。他已经知道如果要去求出一个n个点、m条边的无向图的最小生成树有一个Krustal算法和另一个Prim的算法。另外,他还知道,某一个图可能有多种不同的最小生成树。例如,下面图 3中所示的都是图 2中的无向图的最小生成树:
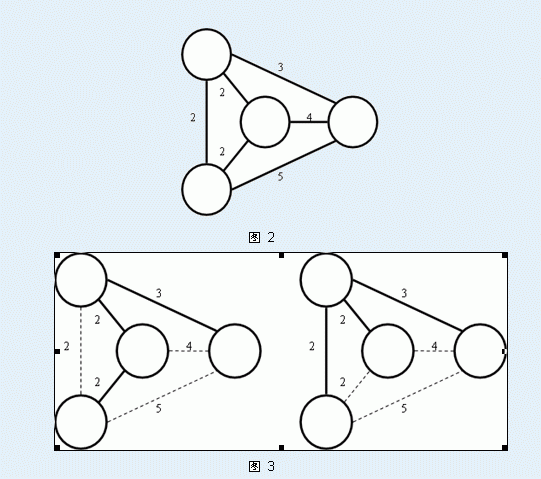
当然啦,这些都不是今天需要你解决的问题。Secsa想知道对于某一条无向图中的边AB,至少需要多少代价可以保证AB边在这个无向图的最小生成树中。为了使得AB边一定在最小生成树中,你可以对这个无向图进行操作,一次单独的操作是指:先选择一条图中的边 P1P2 ,再把图中除了这条边以外的边,每一条的权值都减少1。如图 4所示就是一次这样的操作:
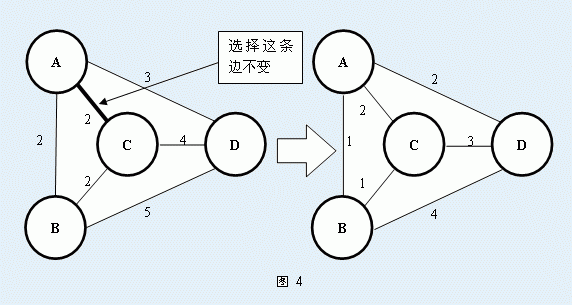
输入格式
输入文件的第一行有3个正整数n、m、Lab分别表示无向图中的点数、边数、必须要在最小生成树中出现的AB边的标号。
接下来m行依次描述标号为1,2,3…m的无向边,每行描述一条边。每个描述包含3个整数x、y、d,表示这条边连接着标号为x、y的点,且这条边的权值为d。
输入文件保证1<=x,y<=N,x不等于y,且输入数据保证这个无向图一定是一个连通图。
输出格式
输出文件只有一行,这行只有一个整数,即,使得标号为Lab边一定出现最小生成树中的最少操作次数。
4 6 1
1 2 2
1 3 2
1 4 3
2 3 2
2 4 4
3 4 5
1
数据范围与约定
第1个样例就是问题描述中的例子。
1<=n<=500,1<=M<=800,1<=D<10^6

