#PBZOJ2267. Telephone Network
Telephone Network
题目描述
Telephone Network
A telephone company wants to build a new telephone network in a city. The company has the goal that each person in the city should be able to call each other person. Of course, it is not possible to build direct connections between every pair of persons. Instead, the company uses a network made up of several layers.
We denote a network switch in layer j by S(j). A switch S(0) consists of one input, one output and a cable connecting the input to the output. A switch S(j) with j > 0 consists of 2j inputs, 2j outputs and two switches S(j−1). Input i of S(j) (0 ≤ i < 2j) is connected via a cable to the inputs i mod 2j−1 of each of the two switches S(j−1). Similarly, output i of S(j) is connected to the outputs i mod 2j−1 of each of the two switches S(j−1).
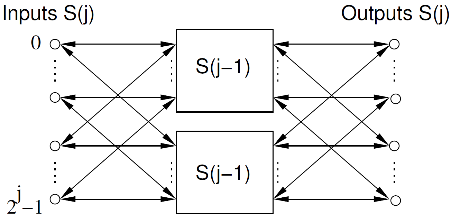
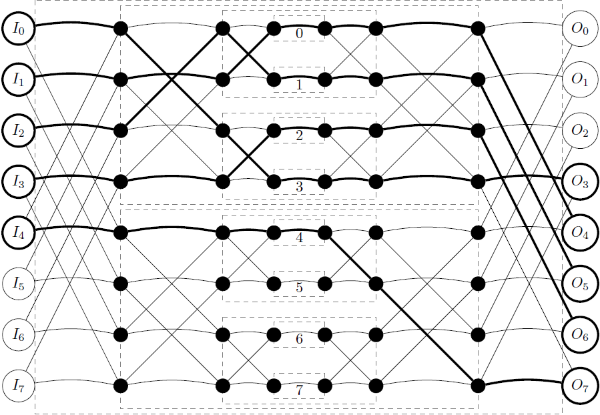
We are considering a network with one switch S(n) in the outermost layer. It can be shown that any input and output of switch S(n) has a unique connection path to any of the S(0) switches. Therefore, any input of S(n) can be connected to any of its outputs, and the connection path is uniquely determined by specifying through which switch S(0) the connection is established.
We number the switches S(0) belonging to the switch S(n) from 0 to 2n−1. The i-th switch S(0) is defined as follows. Write the number i in binary as bn−1bn−2…b0. This defines a path from an input of S(n) to the i-th switch S(0) via the following procedure: for each j, bj=0 indicates that the path extends from S(j+1) to the first S(j) switch to which it is directly connected, and bj=1 indicates that the path extends to the second S(j) switch. Note that regardless of which input of S(n) is selected, this path arrives at the same S(0) switch, which is given the number i. See also the figure below the sample data for details of how the numbering works.
Sometimes multiple connections are needed at the same time. In order to avoid interference, each of the inputs and outputs of all switches S(j) (0 ≤ j ≤ n) can be used by at most one connection. Given a set of connection requests, can you find connection paths for each request such that the connection paths are disjoint?
最外层网络只有一个开关S(n)。对已S(n)的任意一个输入和输出,他们都有一条独特的路径连接到S(0)。因此,任意一个输入和输出就能够连接起来,而且这样的路径是独一无二的有连接到S(0)的路径决定的。我们将S(n)的2n 个S(0)级开关标号为0- 2n−1。第i个开关的定义为:将i写成二进制 bn−1bn−2…b0. 。S(n)到S(0)的路径是这么确定的:对于每一位j,bj=0 就表示S(J+1)连接到第一个S(j)开关,否则连接到第二个S(j)开关。对于给定的i,无论开关S(n)的输入是什么,这个路径必须到达同一个S(0)开关。不懂的就好好看样例。有时候多组连接必须同时使用,为了防止交叉干扰,每个开关只能在这些通话中使用一次。给你一些通话需求,你能找到满足所有要求且不相交的路径么?
输入格式
On the first line a positive integer: the number of test cases, at most 100. After that per test case:
- One line with two integers n (1 ≤ n ≤ 16) and m (1 ≤ m ≤ 2n): the layer of the outermost switch and the number of connection requests.
- m lines, each with two integers ai and bi (0 ≤ ai, bi < 2n). Each such line represents a connection request from input number ai of S(n) to output number bi. You may assume that the integers ai are pairwise distinct, and the integers bi are pairwise distinct as well.
第一行一个正整数,表示测试数据,最多100组。
然后每一组包括:
· 第一个两个数n (1 ≤ n ≤ 16),m (1 ≤ m ≤ 2n):网络的层数和连接需求数。
· 接下来m行,每行包括两个正整数ai 和bi (0 ≤ ai, bi < 2n). 表示输入和输出的编号。Ai和bi只会出现一次。
输出格式
Per test case:
- One line with m integers s1, …, sm, where si is the number of the S(0) switch through which the connection of input ai to output bi is established.
The connection paths should be disjoint. You may print any valid solution, and you may assume that there is at least one valid solution.
Per test case:
· M个正整数s1, …, sm, si是ai到bi的连接路径。
连接必须不想交。输出人任意一个合法路径,,并且路径是存在的。
2
1 1
0 1
3 5
0 3
1 4
2 5
3 6
4 7
0
3 0 1 2 4
Hint
3 5 ---3层网络,5个连接
0 3
1 4
2 5
3 6
4 7
输入就这样了
输出
第一个3
二进制表示为011
表示0先连最外层的第一个开光,下一层是第二个,在下层第二个。这样就连接到最底层
图上每一个圈都有两条线
选0时就是上面一条,选1就是下面一条
数据范围与约定